데이터 시각화에서의 색상 활용
- 2024-09-08 (modified: 2025-06-28)
- 출판일: 2014-05-06
- 저자: AK
데이터 시각화 맥락에서 색을 어떻게 사용하면 좋을지 정리했다.
색을 사용하는 두 가지 용도
지나치게 단순화하는 감이 있지만 색상을 사용하는 용도는 S. S. Stevens의 Level of measurement에 기반하여 다음과 같이 크게 둘로 나눠볼 수 있다.:
- 서로 다른 종류를 구분하기 (nominal or categorical scale)
- 정도의 차이를 나타내기 (ordinal, interval, ratio scale)
예를 들어 지하철 1, 2, 3, 4호선이 있다. 1, 2, 3, 4는 숫자이지만 아무도 2호선과 4호선이 두 배 차이라거나, 1호선과 3호선이 3배 차이라거나 하는 식으로 계산하지 않는다. 숫자는 숫자이지만 사실은 “서로 다르다”는 것 이외에는 아무런 의미가 없다. (개통 순서를 나타내기는 하지만 이용자 입장에서 전혀 중요하지 않으므로 무시)
이런 식으로 종류를 구분하기 위해 쓰는 숫자를 nominal data 혹은 categorical data라고 부른다. 이러한 데이터를 색으로 나타낼 때에는 색조(hue)의 차이를 사용하는 것이 좋다. 특히 범문화권적으로 사람들이 쉽게 인지하고 기억할 수 있는 색상은 아래와 같다:
- 검은색
- 흰색
- 빨간색
- 녹색
- 노란색
- 파란색
위 색상 순서는 문화인류학적 연구를 통해서도 검증된 바 있고, 생리학적 기반을 갖고 있기도 하다(1차 시각 피질에서 일어나는 Color-opponent processing 연산). 단, 적녹색명인 경우 녹색과 빨간색의 구분에 어려움을 겪으므로 사용에 주의할 것.
이와 달리 물의 온도, 등수, 백분율, 몸무게 등 “크기” 혹은 “순서”의 개념이 있는 숫자들을 ordinal이라고 부른다(order의 ord-). 좀 더 정확히는 위 숫자들을 ordinal, interval, ratio 등으로 나누기도 하는데 이에 대해서는 Level of measurement 참고.
순서가 있는 숫자인 경우 색조 차이를 이용하기 보다는 명도나 채도 차이를 이용하는 것이 좋다. 이 때 자연스러운 매핑은 큰 숫자일수록 배경색과의 대비가 커지도록 만드는 것이다. 예를 들어 밝은 빨강에서부터 점점 명도를 낮춰서 어두워지는 스케일을 사용하고 했을 때, 배경이 어둡다면 가장 큰 수에 밝은 빨강을, 배경이 밝은 빨강이면 가장 큰 수에 어두운 빨강을 할당하는 것이 자연스럽다.
아래 그림에서 가운데 회색조 부분을 보자. 검정색이 큰 수를 나타낼까, 흰색이 큰 수를 나타낼까? 하나의 답은 없고, 배경과의 대비가 큰 색이 큰 수를 나타낸다고만 말할 수 있다:

색공간, 두 색 사이의 거리
위의 예시에 덧붙여서 색공간 개념을 설명해보고자 한다.
물리적으로 색이라는 것은 결국 빛의 파장과 세기라는 두 개의 차원으로 구성된다. 밝기(빛의 세기)를 고정하면 파장만 남으므로 색상(hue)이라는 것은 사실 1차원이다. 하지만 우리 눈에서 색상을 인식하는 광 수용체(cones)가 세 종류(Long, Medium, Short range)라서 우리는 색상을 다차원으로 인식한다:
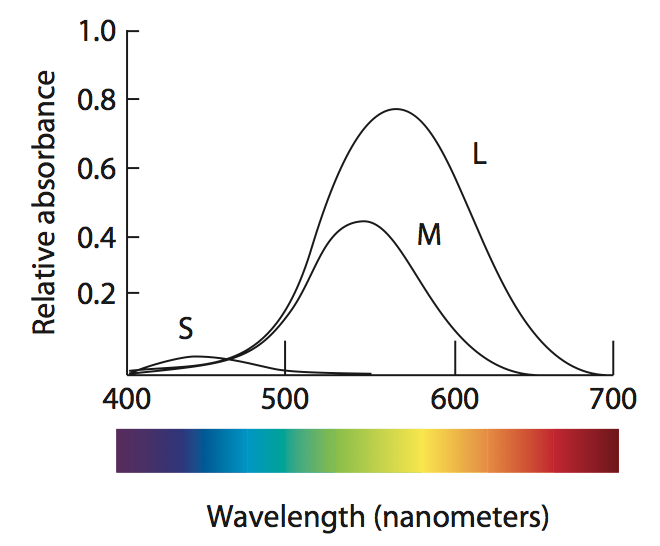
위 그림은 세 종류의 광 수용체가 반응하는 파장의 영역(x축)과 빛을 흡수하는 정도(y축)를 나타낸다. 재미난 점은 L-type이 M-type의 영역을 거의 다 포함한다는 점, S-type의 흡수량이 대단히 적다는 점이다.
이게 시각화랑 무슨 상관인가?
대단히 많은 영향이 있다. 일단, 파란색 빛과 노란색 빛이 동일한 강도로 눈에 주입되었을 때 파란색 빛은 상대적으로 약하게 느껴질 것이다(S-type cone의 그래프를 보라). 반면 노락색 빛은 M-type과 L-type 모두를 자극하기 때문에 두 cone들이 미친듯이 발화하여 시각피질이 있는 뒷통수로 신호를 보낼 것이다. 게다가 시각피질에서는 아래 그림에서와 같이 M-type과 L-type에서 보내는 신호를 합쳐서 White-Black 채널을 만들고 여기에서 S-type의 신호를 빼서 Yellow-Blue 채널을 채널을 만들어낸다:
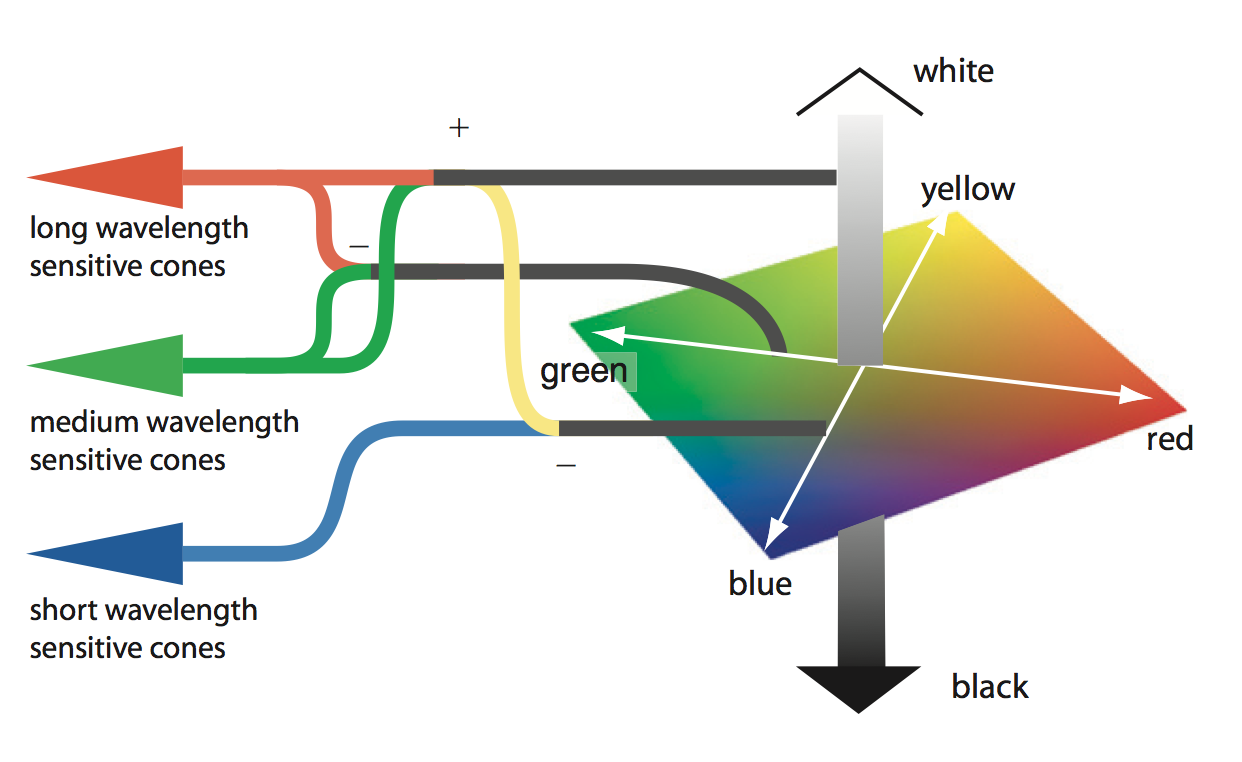
검은 배경(검은색은 기본적으로 빛이 없는 상태를 말한다)에 파란 글씨가 잘 안보이는 반면, 노란 글씨는 잘 보이는 이유다.
이런 식의 왜곡으로 인해 색 공간에도 왜곡이 필요하다.
우리에게 친숙한 HSV 색공간의 경우 자세히 보면 노란색 부분이 특히 밝아서 수직으로 기둥 같은 것이 보이고, 파란색 부분은 특히 어두워서 수직 기둥이 보이는 등 분포가 고르지 않음을 알 수 있다. 물리적으로는 정확하지만 우리 눈에 왜곡이 있어서 나타나는 현상이다.
우리 눈에 맞춰 고의적으로 왜곡을 시킨 CIE-LAB 색공간의 단면에서는 전체적으로 색 분포가 고르지만 좀 더 탁해보인다. 그 이유는 가장 밝은 노란색에 해당하는 파란색이 없기 때문에 색 공간을 사각형에 맞추기 위해 가장 밝은 노란색 부분을 짤라내는 식으로 왜곡이 일어났기 때문이다.
이제 드디어 지각적으로 올바른 두 색 사이의 거리에 대해 이야기할 수 있게 되었다. 종류를 구분하기 위해 색을 선택하는 경우(nominal)에는 CIELAB 색공간에서 y축을 고정하고 x축으로 이동하며 색을 뽑으면 된다. 순서나 크기의 차이를 나타내기 위해 색을 선택하는 경우 CIELAB 색공간에서 y축으로 등간격으로 이동하며 색을 뽑으면 된다.
간단한 결론은, 데이터 시각화에서 사용할 색을 고를때는 CIELAB 또는 거기에서 파생된 색공간을 쓰는 것이 좋다는 것이다.
깊이 지각 및 상세한 차이를 표현하기
위에서 잠깐 언급한 Color-opponent processing의 결과로 세 쌍의 색상 채널이 만들어진다. 이 중 두 축(yellow-blue, green-red)은 색상 채널(chromatic channels)이고, 한 축(black-white)은 밝기 채널(luminance channel)이다.
(아마도 진화적인 이유로) 밝기 채널은 시야에 잡히는 그림자 정보로부터 표면의 모양을 표현하는 일을 처리하는 것에 최적화되어 있는 반면 색상 채널은 그렇지 못하다. 예를 들어 동일한 정보를 색상 채널로만 처리하는 경우와 밝기 채널로만 처리하는 경우 지대한 차이가 나타난다.
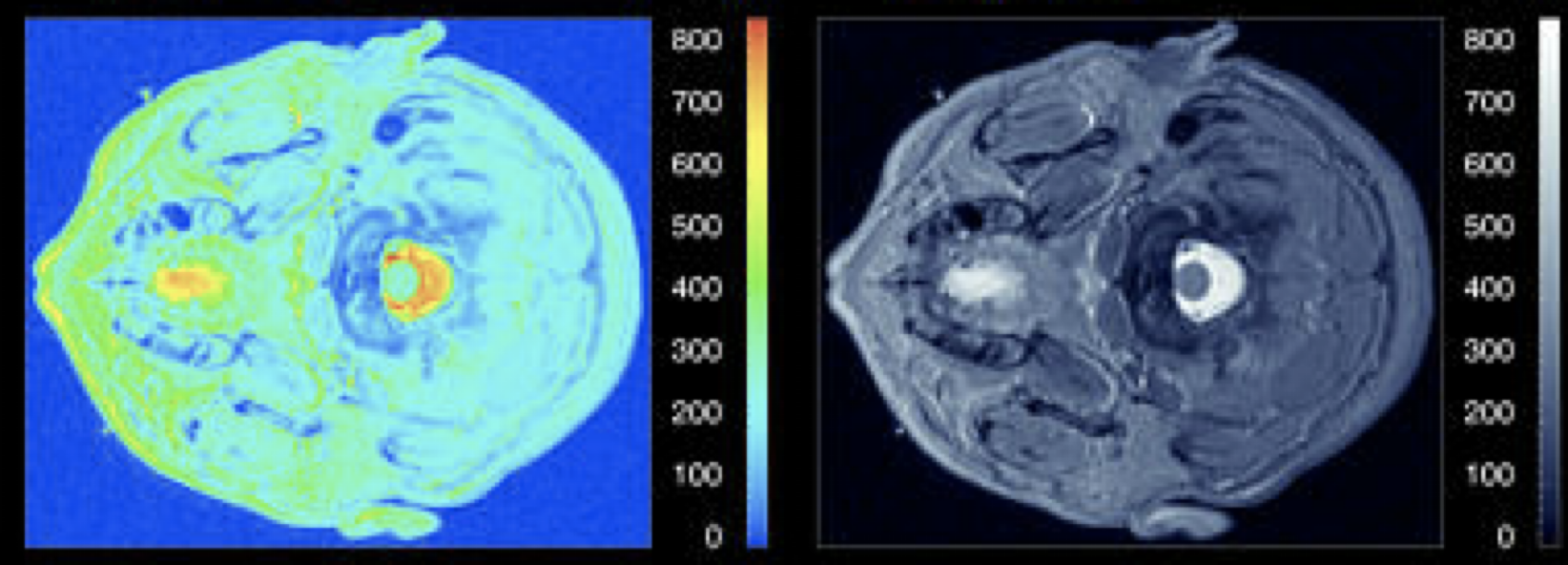
따라서 2차원 공간 상에서 색상을 이용하여 높이 값을 표현할 때, 무지개색(rainbow color coding)을 쓰는 것에 비해 명도 채널을 활용하는 것이 디테일을 훨씬 더 잘 살릴 수 있다.
시간과 거리
마지막으로 하나만 더.
최근 2년 간의 매출 변화를 그래프로 어떻게 그리면 좋을까? 2010, 2011, 2012라는 시간의 흐름에는 순서가 있다. 순서가 있으니 최소 ordinal scale이고, 따라서 명도나 채도 차이를 이용하는 것이 좋을 것이다. 이 때, 2010년을 진한색으로 할 것인지, 2012년을 진한색으로 할 것인가를 어떻게 정하는게 좋을까?
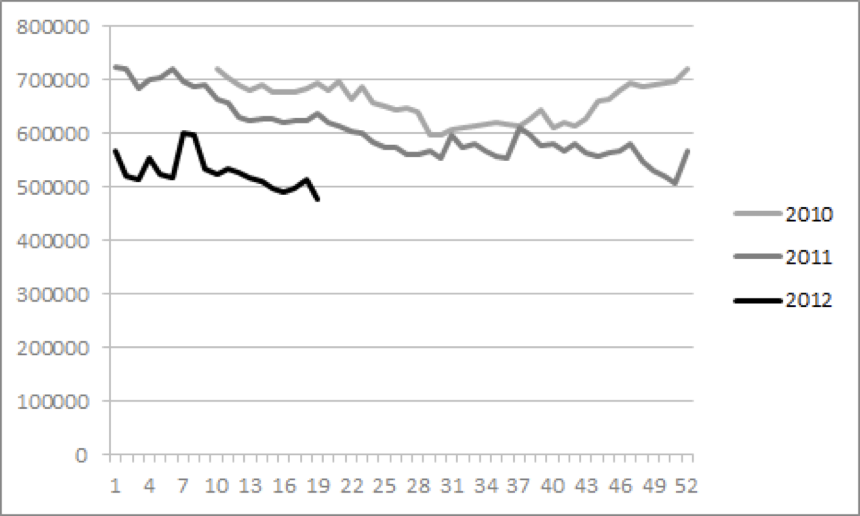
내 생각엔 메타포와 멘탈 스키마에 대한 George Lakoff나 Mark Turner 등의 연구가 도움이 되는 것 같다. 이들의 연구에 의하면 공간 상에서의 거리와 시간 상에서의 선/후 관계는 하나의 스키마로 호환이 된다. 먼 거리는 현재로부터 멀리 떨어진 시간(과거이건 미래이건)을 뜻한다. 멀리에 있는 사물은 흐리게 보인다. 따라서, 현재로부터 먼 과거를 흐린 색으로 매핑하면 자연스럽다.